|
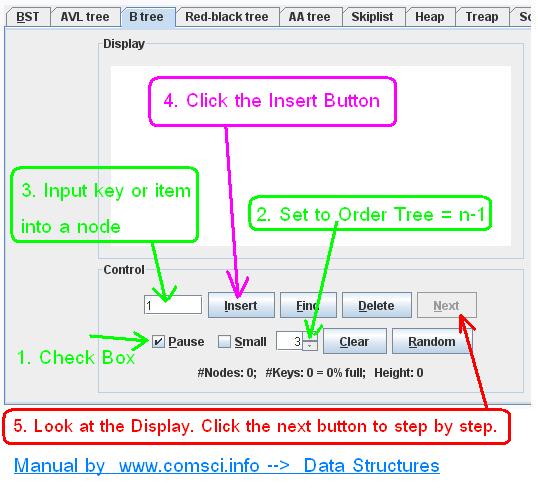
This applet animates the functioning of several dictionary data structures. It can be used as a teaching aid or for self-study. By watching the visualization the user should more easily grasp the ideas behind the data structures.
URL : http://people.ksp.sk/~kuko/bak
The Website comsci.info is create to the B-Trees Example.
Please look at to this webpage...
B-Trees Example1 :

In this first example(1), we assume that the order size1 is 3 and that there are a maximum of two keys in each leaf node and a node. Insert sequence : 1, 2, 3, 4, 5, 6, 7, 8, 9, 15, 16, 17, 18, 20, 30, 40
Height increases by 1 or
Inserting Key Value 1 :

The tree is empty so we make a new root.
Inserting Key Value 2 :

We start at the root.
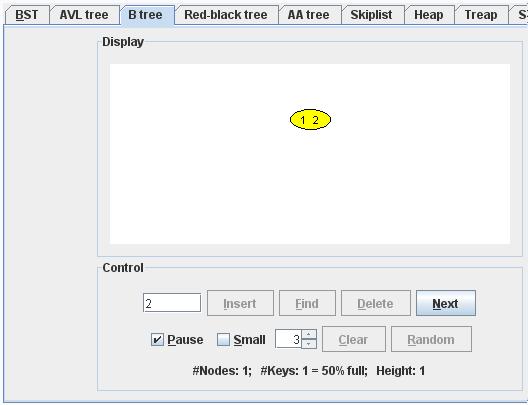
We insert the key into this node.
Inserting Key Value 3 :

We start at the root.
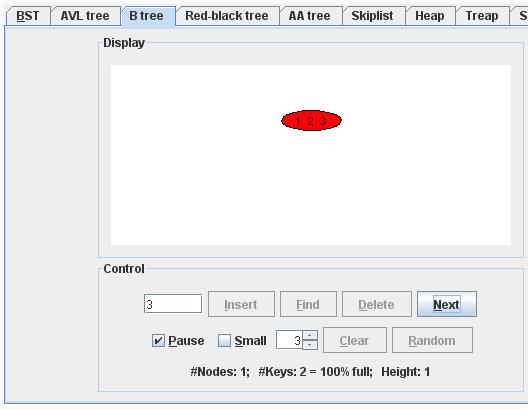
We insert the key into this node.

The node is too big, we have to split it.
Inserting Key Value 4 :
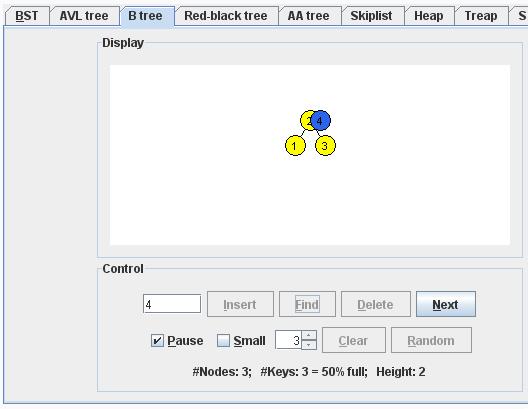
We start at the root.
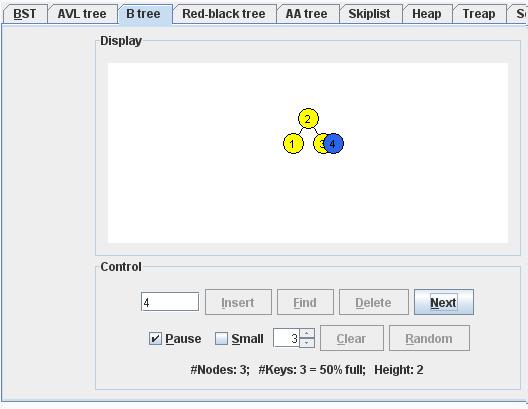
2 < 4, we go along the 2. link.

We insert the key into this node.
Inserting Key Value 5 :

We start at the root.
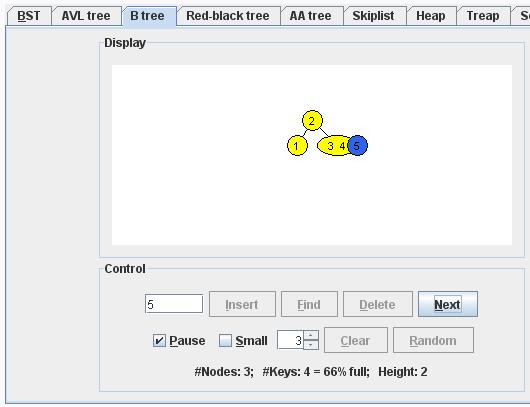
2 < 5, we go along the 2. link.

We insert the key into this node.

The node is too big, we have to split it.

The node is too big, we have to split it.

The node is too big, we have to split it.
Inserting Key Value 6 :

Inserting Key Value 7 :

We start at the root.

4 < 7, we go along the 3. link.
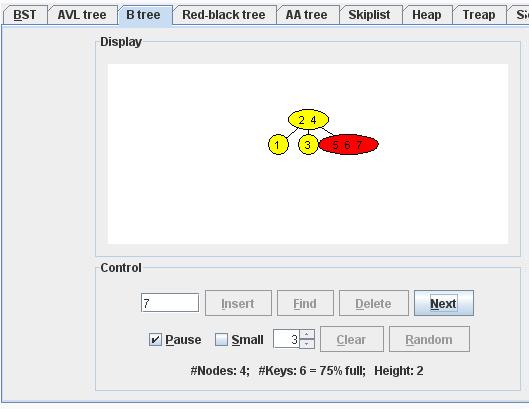
We insert the key into this node.

The node is too big, we have to split it.

The node is too big, we have to split it.

The node is too big, we have to split it.

Inserting Key Value 8 :

Inserting Key Value 9 :
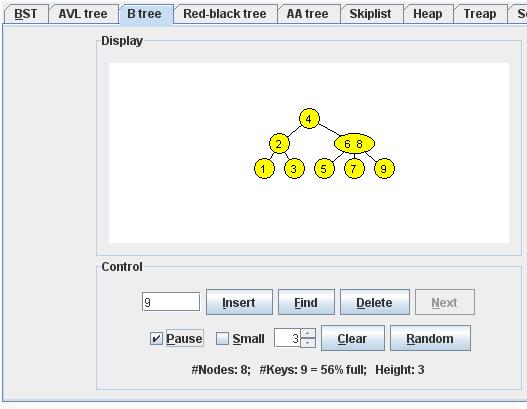
Inserting Key Value 15 :

Inserting Key Value 16 :

Inserting Key Value 17 :
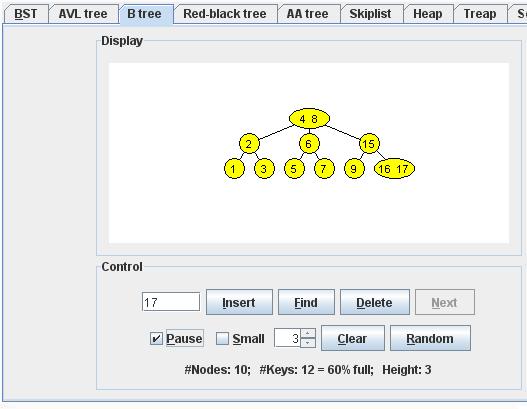
Inserting Key Value 18 :
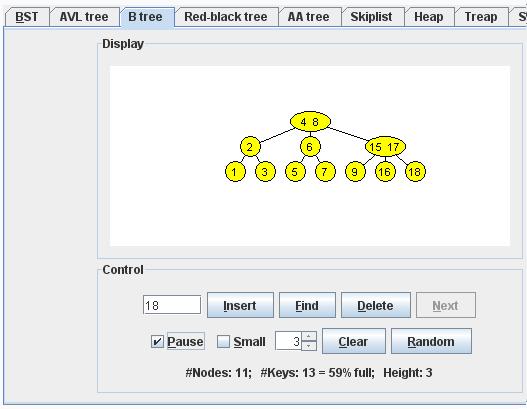
Inserting Key Value 20 :

Inserting Key Value 30 :
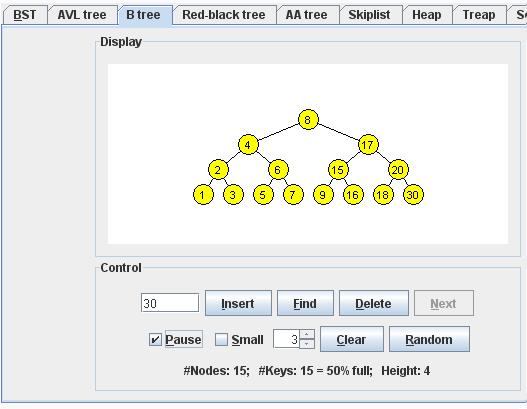
Inserting Key Value 40 :

Algorithms Summary in B- Tree and B+ Tree
Algorithms Summary in B- Tree
----------------------------------------------------------------
Search(T, k)
//Search a B-Tree, T, for a key, k.
//if found k then return pointer to node containing k
//else return NULL
current_node = root(T)
While current_node is not NULL
Search through keys in current_node until
1. found k
2. found first key (ki) larger than k or
3. passed last key in current_node
Case 1.
return pointer to current_node
Case 2.
current_node = ith child of current_node
Case 3.
current_node = last child of current_node
End While
return NULL
// NOTE: A recursive version of the above is given in the text.
----------------------------------------------------------------
B-Tree-Split-Child(x, i, y)
//Splits a node, y, in a B-Tree and moves y's median key up to y's parent, x.
//y is the ith child of x.
//This function will only be called if y is full; i.e., has 2t-1 keys.
Allocate a new node and call it z. //z will be the new sibling of y.
If y is a leaf then mark z as a leaf, else mark z as an internal node.
set the number of keys in z to t-1
copy the last t-1 keys of y into z.
if z is not a leaf then copy the last t pointers of y into z.
set the number of keys in y to t-1
insert a (child) pointer to node z into node x.
insert the original middle key of node y up into node x, moving other keys and pointers as necessary
increment the number of keys in x by one.
Update x, y and z on disk.
----------------------------------------------------------------
B-Tree-Insert(T, k)
//Insert the key, k, into tree, T.
r = root[T]
if the root is full (i.e., has 2t-1 keys) then
Allocate a new node and call it s. //s will be the new root.
root[T] = s //make s the root. r still points to original root.
set the number of nodes in s to 0.
set the only child pointer of s (c1[s]) to point to r. //r is now the child of s.
call B-Tree-Split-Child(s, 1, r) to split r and move its middle key up into s.
call B-Tree-Insert-NonFull(s, k) to insert the key, k, into the B-Tree with root, s.
else //root is not full
call B-Tree-Insert-NonFull(r, k) to insert the key, k, into the B-Tree with root, r.
end if
----------------------------------------------------------------
B-Tree-Insert-NonFull(x, k)
//Inserts the key, k, into a B-Tree. (k will ultimately be inserted into a leaf).
//Begin by attempting to insert k into nonfull node, x.
i = the number of keys in x.
if x is a leaf then
since x is not full insert k into its proper place in x.
add one to the number of keys in x and update x on disk.
else //x is not a leaf
Move back from the last key of x until find child pointer to node
that is root of subtree in which k should be placed.
if this child node is full then call B-Tree-Split-Child(x, i, ci[x])
//Note: we split full nodes on the way down the tree so that if a child of that
//node needs to be split its parent will be able to accept the middle key.
set i = index of whichever child of x is root of subtree in which k should be placed.
call B-Tree-Insert-NonFull(ci[x], k) //Note: Recursive call
end if
----------------------------------------------------------------
B-Tree-FindLargest(x)
//x is the root of the subtree to be searched.
//B-Tree-FindLargest returns a pointer to the node containing the largest key in the subtree whose root is x.
current_node = x
while current_node is not a leaf
current_node = largest child node of current_node
end while
return current_node
----------------------------------------------------------------
B-Tree-Delete(x, k)
//k is the key to be deleted and
//x is the root of the subtree from which k is to be deleted.
//B-Tree-Delete returns true if it successfully deletes k else it returns false.
//Note: This function is designed so that whenever it is called recursively x has at least t keys.
if x is a leaf then
if k is in x then
delete k from x and return true
else return false //k is not in subtree
else //x is an internal node
if k is in x then
y = the child of x that precedes k
if y has at least t keys then
k' = the predecessor of k (use B-Tree-FindLargest)
Copy k' over k //i.e., replace k with k'
B-Tree-Delete(y, k') //Note: recursive call
else //y has t-1 keys
z = the child of x that follows k
if z has at least t keys then
k' = the successor of k
Copy k' over k //i.e., replace k with k'
B-Tree-Delete(z, k') //Note: recursive call
else //both y and z have t-1 keys
merge k and all of z into y //y now contains 2t-1 keys.
//k and the pointer to z will be deleted from x.
B-Tree-Delete(y, k) //Note: recursive call
else //k is not in internal node x.
ci[x] points to the root, c, of the subtree that could contain k.
if c has t-1 keys then
if c has an immediate left/right sibling, z, with t or more keys then
Let k1 be the key in x that precedes/follows c.
Move k1 into c as the first/last key in c.
Let k2 be the last/first key in the immediate left/right sibling, z.
Replace k1 in x with k2 from z (i.e., move k2 up into x).
Move the last/first child subtree of z to be the first/last child subtree of c.
else //c and both of its immediate siblings have t-1 keys.
//we cannot descend to a child node with only t-1 keys so
merge c with one of its immediate siblings and
make the appropriate key of x the middle key of the new node, c.
//Note: This may cause the root to collapse, thus making c the new root.
B-Tree-Delete(c, k)
// URL = http://cs-netlab-01.lynchburg.edu/courses/DataStII/BTreeOps.htm
----------------------------------------------------------------
Algorithms Summary in B+ Tree
- Insert Algorithm of B+(Plus) Tree
s = Key value to be inserted
Search tree for node n containing key s with path in stack p
from root(bottom) to parent of node n(top).
IF found THEN
STOP
ELSE
IF n is not full THEN
Insert s into n
ELSE
Insert s in n (* assume n can hold s temporarily *)
j = number of keys in n / 2
Split n to give n and n1
Put first j keys from n in n
Put remaining keys from n in n1
(k,p) = (nk[j],"pointer to n1")
REPEAT
IF p is empty THEN
Create internal node n2
Put (k,p) in n2
finished = TRUE
ELSE
n = POP p
IF n is not full THEN
Put (k,p) in n
finished = TRUE
ELSE
j = number of keys in n / 2
Split n into n and n1
Put first j keys and pointers in n into n
Put remaining keys and pointers in n into n1
(k,p) = (nk[j],"pointer to n1")
END
END
UNTIL finished
END
END
- Delete Algorithm of B+(Plus) Tree
Please wait to upload...
- Search Algorithm of B+(Plus) Tree
Please wait to upload...
// URL = http://www.mec.ac.in/resources/notes/notes/ds/bplus.htm
----------------------------------------------------------------
|

